A quadratic function is also called a quadratic polynomial or a quadratic, and it is a polynomial with one or more variables where the highest degree term is of the second degree. If the quadratic function is set as equal to zero, it is called a quadratic equation. It is important in Algebra to understand quadratic functions and how to identify them.
When you have a quadratic function, you might have one variable, such as x, or you can have multiple variables, including x, y, and z. The most important thing to note is that no variable can be higher than the second degree. This relates to the exponents in the function. For example, if one of the variables is x to the third power, then you would have a third degree polynomial, and it would not be a quadratic function.
Check the Exponents of Each Variable
No matter how many variables are in your function, you need to check each one. If you find that the highest exponent is two, then you have a quadratic function. You can use quadratic functions to solve problems that involve measurements that have unknown variables. For example, if you are building a fence, you could use a quadratic equation to determine the length of the fences by plotting the longest and shortest possible fence sections. This is one of the ways a quadratic function is applied.
Rewrite the Equation in Standard Quadratic Form
No matter how the variables are presented, you can rewrite them in the standard format for a quadratic function. F(x) = y = ax^2 + bx + c is the equation, where a, b, and c are numbers and a is not equal to zero. If it was zero, then the equation would be linear and not quadratic. For example, if you have f(x) = x +9 + 4x^2, you would rewrite the function with the largest exponent first, so you would have f(x) = 4x^2 + x + 9. Since the highest exponent, also called the degree of the polynomial, is 2, it is a quadratic function.
Graph the Equation
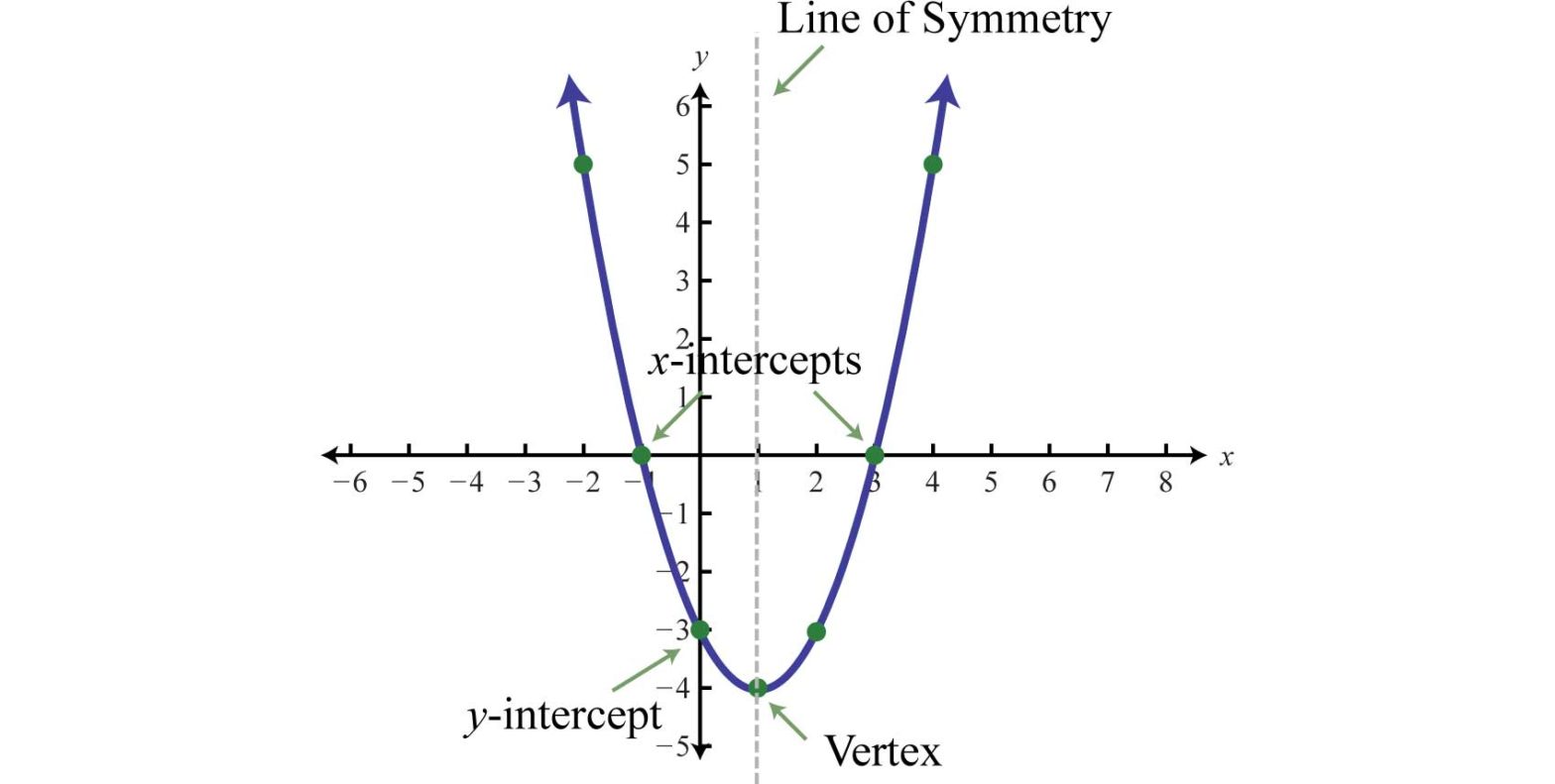
A quadratic function has a domain that is entirely real numbers, so you can graph this function to determine if it is a quadratic function. In addition, it will create a parabola, which is a U-shaped figure, on a graph. The parabola can open up or down. You can take real numbers and substitute them for x, and solve for y.
When you draw the graph, the x coordinate will fall along the x-axis, which goes from left to right. The y coordinate will correspond to the y-axis, which goes up and down. Once you plot a number of points, check to see if you have a parabola. If you do, it is a quadratic function.
Understanding quadratic functions is critical in Algebra, and it is used in many applications in the real world, especially in engineering, science, and business. For example, if you want to know the trajectory of a bouncing ball, you will use a quadratic function. Businesses use them to forecast profit and loss. They are also useful in any field where you need to determine minimum or maximum values.
The simplest example is throwing a ball because gravity causes the ball to go up and then come down, forming an arc. This arc represents the parabola. There is a point at which the ball is as high as it will go before it turns and heads back down. This is called the vertex of the parabola. The parabola starts at the person throwing the ball, reaches the vertex, and then heads downward. A quadratic equation will tell you the trajectory of this ball.
Once you understand the formula and how to arrive at the equation, you will be able to calculate many different things using quadratic functions.